Examining Quantum Computational Complexity and Entropy in Artistic Form

In an era where digital art is rapidly evolving, quantum computation offers an entirely new creative paradigm—one that moves beyond traditional synthesis and generative visuals. By translating quantum states into sound and fractal imagery, we step into an artistic space where complexity is not just computed but felt. The video below captures this interplay of structured randomness: quantum-generated music shaping quantum fractal art, revealing an emergent aesthetic dictated by the very nature of quantum information.

Capturing nature’s intrinsic complexity in artistic form has been an inspirational source for artists across centuries. Our modern day capability to precisely control and capture information from nature’s smallest units, atoms, through the use of quantum computers offers a novel medium to create art. We use quantum computers as inputs to both generate fractal images as well as synthesize sounds in a visual and audio atomic display, see the prototype video below.

Quantum information represents a new technological evolution in artistic creation to generate complex forms using today’s accessible quantum computers. 

Headlines typically display quantum computing utility arising from its ability to exceed the computational capacity of the world’s largest supercomputers in problems related to cryptography, machine learning, chemistry simulation and optimization, further promising an ability to address complex problems facing our world today. Noise arising from quantum computers' environmental sensitivity makes application realization difficult; however, we find that quantum noise enhances the richness and complexity of our art forms. 

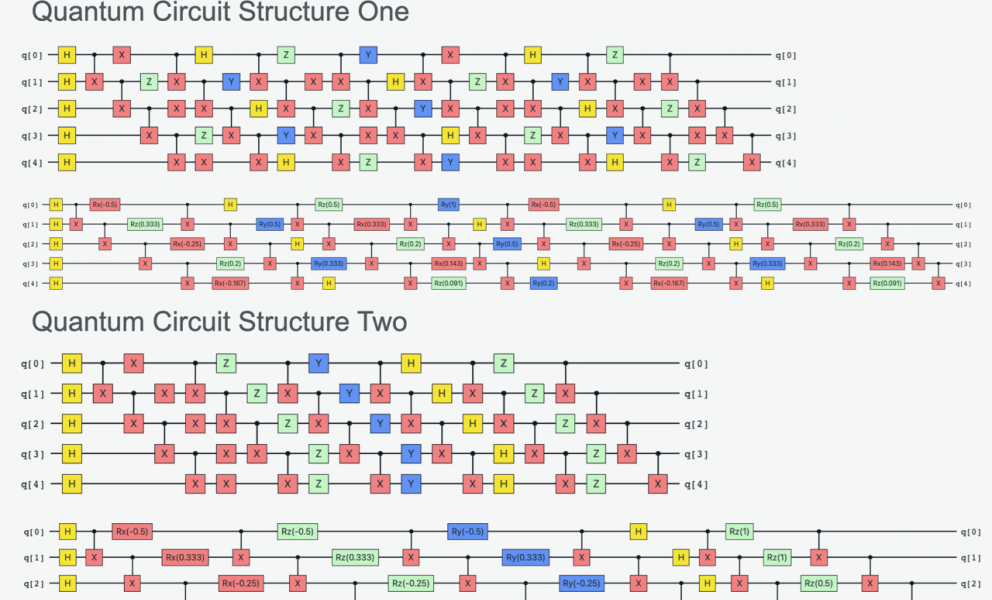
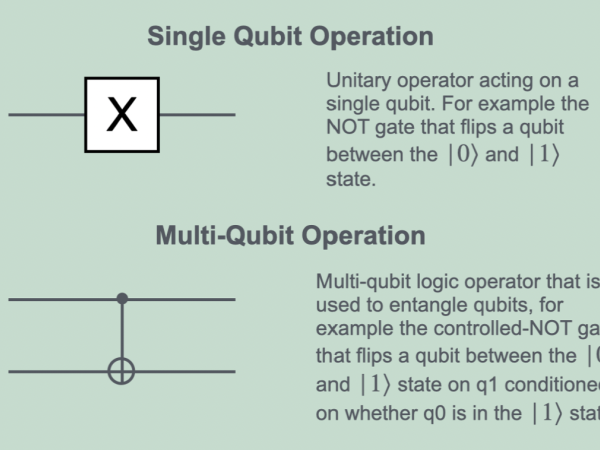
Our creation is rooted in the operations we choose to implement on quantum computers known as quantum circuits. These operations manipulate both the phase and the amplitude of the quantum wave function which describes the probability a quantum system is in a particular state.  Quantum operations are simply categorized as a) single qubit operations and b) multiqubit entangling operations shown in the diagram below. The construction of quantum circuits underpins the artistic output, and the circuits are designed to yield interesting time-evolved wave forms. Consider dancers in a performance as an analogy. A single dancer may twirl and leap independently or they may move together, entangling and correlating movement. We choreograph the qubits, and the quantum dance is expressed through sound and fractals. The dance yields complex structure depending on how we design the quantum circuit.

© Wiktor Mazin

Quantum Music

Abstract parallels exist between music composition and quantum computing. Music compositions combine notes across frequency octaves to construct complex and appealing sound signals, while quantum circuits are composed of quantum operations that construct complex wavefunctions that can describe atomic matter. At the core, both fields employ mathematical constructions to shape complex waveforms. Bridging the quantum waveforms with sound waveforms is done in an analog fashion by imposing quantum computing output onto a sound signal or synthesizer. 

We create a synthesizer algorithmically which provides mathematical flexibility and a tool to create sounds from quantum computing output. Coding music is a growing electronic music domain and is used to construct algorithmic compositions, compositions with artificial intelligence, and interpolate data in musical form. To draw a connection between familiar instruments and mathematical music representations, consider a piano. A piano consists of a key array each representing an independent note tuned to a specified frequency. Pressing a piano key produces a signal, typically a standard ADSR (Attack, Decay, Sustain ,Release) form. The player may press a single key or multiple keys at once which is a chord. Chords are the essence of complex musical tones resulting from the harmony of multiple signals at varying frequencies being played together. This is the essence of our quantum music.

 Quantum computers at the core produce an array of time-evolved signals, similar to a piano. We can capture the signal amplitude by measuring qubit probability amplitudes after performing a set of quantum operations.  Composing quantum circuits provides us with a complex signal array to feed into our synthesizer to produce complex sound signals. We can then compose songs using multiple quantum computing outputs embedded in synthesizers to create an orchestral effect generated by quantum complexity.

Quantum Fractal Art 

Quantum fractal art is a unique fusion of quantum mechanics and visual arts, leveraging the power of quantum algorithms and fractal mathematics to create fascinating, complex patterns. By applying the principles of quantum computing and the self-replicating nature of fractals, we generate intricate, self-similar patterns that visually integrate the probabilistic and multidimensional essence of quantum systems. At its core, quantum fractal art is built upon the wave function and fractal mathematics, which defines infinitely detailed, repeating structures. Using quantum computing, we retrieve the wave function, transform this information into fractal patterns, and digitally render them, allowing us to explore and interpret quantum phenomena through an artistic lens. The resulting artworks weave together symmetries and asymmetries, reflecting the quantum world's intricacies and complexities. This fusion of science and art offers a novel insight into the wonders of quantum mechanics. 

Quantum Complexity 

Quantum computers and the art created by them are technologically and aesthetically rich due to the complex signals quantum operations generate. One may suspect that entangling operations alone are enough to generate complex quantum wave forms; however, it is known that entanglement operations are not enough. Quantum circuits constructed solely of Clifford operations are classically simulatable which is demonstrative of a lack of complexity. Clifford operations are a special mathematical operator subgroup that maps the Pauli group into itself including: the Hadamard gate, the controlled-NOT gate, the phase gate, and all Pauli gates (Wikipedia). 

Non-clifford operations are all the other operators outside this subset which includes single-qubit pauli rotation operators. Circuits composed of both Clifford and non-Clifford operations become classically non-simulatable at large scale, indicative of quantum wave function complexity. We exploit this distinction between non-complex Clifford quantum circuits and complex Clifford quantum circuits to display quantum complexity as art. Quantum complexity manifests as enhanced artistic complexity directly quantified using entropic measures.

Shannon Entropy

Entropy, specifically Shannon entropy, is a measure of complexity in classical systems. Shannon entropy is a known measure of fractal chaos and complexity. It has also been recently proposed as a measure for tone complexity in musical compositions (link)  with Beethovan’s compositions demonstrating higher entropy measures. Note the distinction between entropy measures for classical systems and entropy measures for quantum systems. Our work imposes quantum mechanical waveforms onto classical compositions, so we choose a classical measure for entropy. Entropy is used to quantify and distinguish artistic complexity between art generated with Clifford and non-Clifford quantum circuits.

Global Shannon entropy provides an overall complexity assessment by considering the entire system, while box-based Shannon entropy offers a more granular view by analyzing specific regions or components of the fractal art. This dual approach allows for a comprehensive understanding of the artistic complexity generated by quantum processes. By applying these entropy measures, we can distinguish and compare the intricate patterns produced by different quantum circuits and sounds, highlighting the potential of quantum computing in creating and analyzing complex visual and auditory experiences.

Quantum Generated Art 

Our art is instantiated using two quantum circuit structures that are executed to extract the quantum wave function amplitude and phase. Interchanging between a clifford and non-clifford circuit is simply done by interchanging the Pauli operators with rotational Pauli operators, so that complexity is truly derived from the addition of non-clifford operators rather than the introduction of new entangling operations. Fibonacci and harmonic series patterns were used to rotate the pauli operators. The amplitudes of the wave function are obtained after each circuit layer on a quantum computer while the phases are obtained through classical simulation.

© Wiktor Mazin

We use the Clifford and non-Clifford wave function outputs separately as an input into a simple SinOsc synth composing two separate songs. The complexity of the non-Clifford song is audible compared to the Clifford song possessing a rich structure that is generated from the rotational Pauli operations on the circuit.

Quantum complexity can also be visualized using quantum fractal art. We examine this complexity by generating fractal images directly from the circuit output as well as inputting the audio signal into a quantum processor. The left figures are fractals generated by Clifford quantum circuits and the right figures are fractals generated from complex, non-Clifford quantum circuits. It is visually apparent that the non-Clifford quantum circuits and non-Clifford quantum sounds generate more complex fractal art. This is reflected quantitatively with the non-Clifford fractal images having a larger Shannon entropy than the Clifford fractal images, see the three fractal image pairs below1.

© Wiktor Mazin

© Wiktor Mazin

© Wiktor Mazin

It is slightly less apparent with the images generated from the quantum audio input, but the trend of higher entropy remains, see the triplet of both Clifford and non-Clifford fractal images.

© Wiktor Mazin

The interplay between quantum computing and artistic form marks the emergence of a new creative paradigm. Expressing abstract concepts like entanglement and quantum complexity through art allows us to sensualize the most fundamental structures of nature. As quantum technology evolves, so too will our ability to interact with and shape quantum systems in ever more intricate ways. Our work lays a few foundational bricks for future artistic expression rooted in the control of quantum dynamics. We shape quantum systems, and through artistic form, quantum systems shape us.

Authors (alphabetical): Mekena McGrew and Wiktor Mazin. 
Disclaimer: This article reflects the authors’ point of view.

• 1Each image pair is generated using the same fractal mathematics, and colors are removed to not influence the entropy calculations.