Untersuchung von Quantencomputer-Komplexität und Entropie in künstlerischer Form

In einer Zeit, in der sich die digitale Kunst rasant weiterentwickelt, bietet die Quantenberechnung ein völlig neues kreatives Paradigma – eines, das über die traditionelle Synthese und generative Bilder hinausgeht. Indem wir Quantenzustände in Klang und fraktale Bilder übersetzen, betreten wir einen künstlerischen Raum, in dem Komplexität nicht nur berechnet, sondern auch gefühlt wird. Das folgende Video fängt dieses Zusammenspiel von strukturiertem Zufall ein: Quantengenerierte Musik, die Quantenfraktalkunst formt und eine entstehende Ästhetik offenbart, die von der Natur der Quanteninformation selbst bestimmt wird.

Die der Natur innewohnende Komplexität in künstlerischer Form zu erfassen, war über Jahrhunderte hinweg eine Inspirationsquelle für Künstler. Unsere heutige Fähigkeit, Informationen aus den kleinsten Einheiten der Natur, den Atomen, durch den Einsatz von Quantencomputern präzise zu kontrollieren und zu erfassen, bietet ein neuartiges Medium zur Schaffung von Kunst. Wir verwenden Quantencomputer als Eingabegeräte, um sowohl fraktale Bilder zu erzeugen als auch Klänge in einer visuellen und akustischen Atomdarstellung zu synthetisieren (siehe das Prototyp-Video unten).

Die Quanteninformation stellt eine neue technologische Entwicklung im künstlerischen Schaffen dar, um mit den heute zugänglichen Quantencomputern komplexe Formen zu erzeugen.

In den Schlagzeilen wird der Nutzen der Quanteninformatik in der Regel damit begründet, dass sie die Rechenkapazität der größten Supercomputer der Welt bei Problemen im Zusammenhang mit Kryptografie, maschinellem Lernen, chemischer Simulation und Optimierung übertreffen kann, was die Lösung komplexer Probleme unserer heutigen Welt verspricht. Das Rauschen, das sich aus der Umgebungsempfindlichkeit von Quantencomputern ergibt, erschwert die Umsetzung von Anwendungen; wir finden jedoch, dass Quantenrauschen den Reichtum und die Komplexität unserer Kunstformen erhöht.

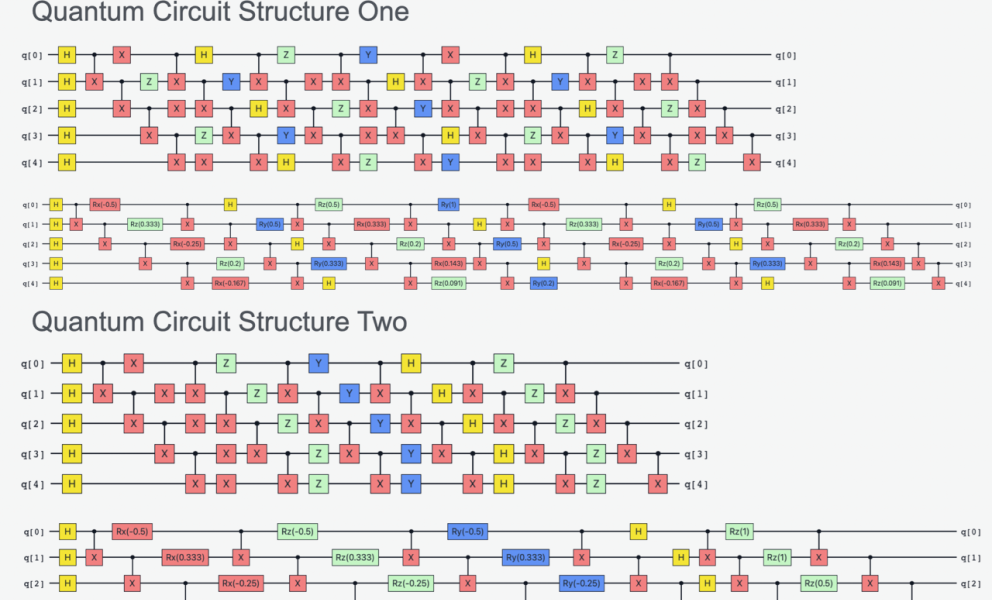
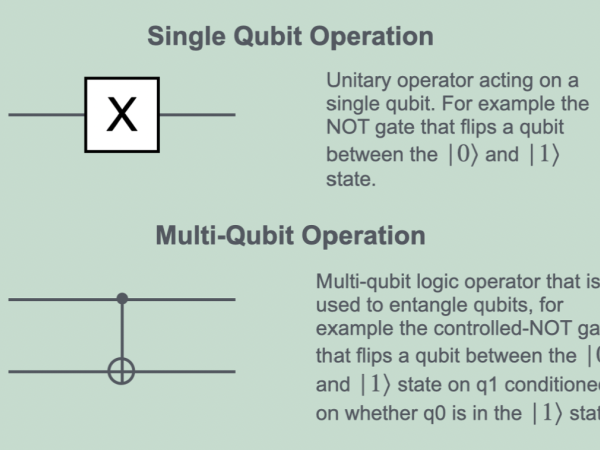
Unsere Schöpfung hat ihre Wurzeln in den Operationen, die wir auf Quantencomputern, den so genannten Quantenschaltkreisen, implementieren wollen. Diese Operationen manipulieren sowohl die Phase als auch die Amplitude der Quantenwellenfunktion, die die Wahrscheinlichkeit beschreibt, mit der sich ein Quantensystem in einem bestimmten Zustand befindet.  Quantenoperationen werden einfach in a) Ein-Qubit-Operationen und b) Multi-Quibit-Verschränkungsoperationen eingeteilt, wie im folgenden Diagramm dargestellt. Die Konstruktion von Quantenschaltkreisen untermauert die künstlerische Leistung, und die Schaltkreise sind so konzipiert, dass sie interessante zeitlich veränderliche Wellenformen ergeben. Betrachten Sie als Analogie die Tänzer in einer Aufführung. Ein einzelner Tänzer kann sich unabhängig voneinander drehen und springen, oder er kann sich gemeinsam bewegen, wobei er seine Bewegungen verschränkt und korreliert. Wir choreografieren die Qubits, und der Quantentanz wird durch Klang und Fraktale ausgedrückt. Je nachdem, wie wir den Quantenkreislauf gestalten, ergibt der Tanz eine komplexe Struktur.

© Wiktor Mazin

Quantenmusik

Es bestehen abstrakte Parallelen zwischen Musikkomposition und Quantencomputing. Musikkompositionen kombinieren Noten über Frequenzoktaven hinweg, um komplexe und ansprechende Tonsignale zu konstruieren, während Quantenschaltungen aus Quantenoperationen bestehen, die komplexe Wellenfunktionen konstruieren, die atomare Materie beschreiben können. Im Kern verwenden beide Bereiche mathematische Konstruktionen, um komplexe Wellenformen zu formen. Die Verknüpfung der Quantenwellenformen mit Klangwellenformen erfolgt auf analoge Weise, indem die Quantencomputerleistung auf ein Tonsignal oder einen Synthesizer übertragen wird. 

Wir erstellen einen Synthesizer auf algorithmischer Basis, der mathematische Flexibilität und ein Werkzeug zur Erzeugung von Klängen aus Quantencomputerdaten bietet. Die Kodierung von Musik ist ein wachsender Bereich der elektronischen Musik und wird verwendet, um algorithmische Kompositionen, Kompositionen mit künstlicher Intelligenz und Interpolationen von Daten in musikalischer Form zu erstellen. Um eine Verbindung zwischen vertrauten Instrumenten und mathematischen Musikrepräsentationen herzustellen, betrachten wir ein Klavier. Ein Klavier besteht aus einer Reihe von Tasten, von denen jede eine unabhängige Note darstellt, die auf eine bestimmte Frequenz gestimmt ist. Das Drücken einer Klaviertaste erzeugt ein Signal, typischerweise eine Standard-ADSR-Form (Attack, Decay, Sustain, Release). Der Spieler kann eine einzelne Taste oder mehrere Tasten auf einmal drücken, was einen Akkord darstellt. Akkorde sind die Essenz komplexer musikalischer Töne, die sich aus der Harmonie mehrerer Signale mit unterschiedlichen Frequenzen ergeben, die zusammen gespielt werden. Dies ist die Essenz unserer Quantenmusik.

 Quantencomputer erzeugen im Kern eine Reihe von zeitlich veränderlichen Signalen, ähnlich wie ein Klavier. Wir können die Signalamplitude erfassen, indem wir die Qubit-Wahrscheinlichkeitsamplituden nach der Durchführung einer Reihe von Quantenoperationen messen.  Durch das Zusammensetzen von Quantenschaltungen erhalten wir eine komplexe Signalanordnung, die wir in unseren Synthesizer einspeisen können, um komplexe Klangsignale zu erzeugen. Wir können dann Lieder komponieren, indem wir mehrere in Synthesizer eingebettete Quantencomputerausgänge verwenden, um einen durch Quantenkomplexität erzeugten orchestralen Effekt zu erzielen.

Quantenfraktale Kunst 

Quantenfraktalkunst ist eine einzigartige Verschmelzung von Quantenmechanik und bildender Kunst, bei der die Kraft von Quantenalgorithmen und fraktaler Mathematik genutzt wird, um faszinierende, komplexe Muster zu schaffen. Durch die Anwendung der Prinzipien des Quantencomputings und der selbstreplizierenden Natur von Fraktalen erzeugen wir komplizierte, selbstähnliche Muster, die das probabilistische und multidimensionale Wesen von Quantensystemen visuell integrieren. Die Quantenfraktalkunst basiert im Kern auf der Wellenfunktion und der fraktalen Mathematik, die unendlich detaillierte, sich wiederholende Strukturen definiert. Mithilfe von Quantencomputern rufen wir die Wellenfunktion ab, wandeln diese Informationen in fraktale Muster um und geben sie digital wieder, so dass wir Quantenphänomene durch eine künstlerische Linse erforschen und interpretieren können. Die daraus resultierenden Kunstwerke verweben Symmetrien und Asymmetrien und spiegeln die Feinheiten und Komplexität der Quantenwelt wider. Diese Verschmelzung von Wissenschaft und Kunst bietet einen neuen Einblick in die Wunder der Quantenmechanik.

Quantenkomplexität 

Quantencomputer und die von ihnen geschaffene Kunst sind aufgrund der komplexen Signale, die durch Quantenoperationen erzeugt werden, technologisch und ästhetisch reichhaltig. Man könnte vermuten, dass Verschränkungsoperationen allein ausreichen, um komplexe Quantenwellenformen zu erzeugen; es ist jedoch bekannt, dass Verschränkungsoperationen nicht ausreichend sind. Quantenschaltungen, die nur aus Clifford-Operationen bestehen, sind klassisch simulierbar, was ein Beweis für die fehlende Komplexität ist. Clifford-Operationen sind eine spezielle mathematische Operator-Untergruppe, die die Pauli-Gruppe auf sich selbst abbildet. Dazu gehören: das Hadamard-Tor, das Controlled-NOT-Tor, das Phasen-Tor und alle Pauli-Tore (Wikipedia).

Nicht-Clifford-Operationen sind alle anderen Operatoren außerhalb dieser Untergruppe, zu der auch die Ein-Qubit-Pauli-Rotationsoperatoren gehören. Schaltkreise, die sowohl aus Clifford- als auch aus Nicht-Clifford-Operationen bestehen, werden auf großer Skala klassisch nicht simulierbar, was auf die Komplexität der Quantenwellenfunktion hinweist. Wir nutzen diese Unterscheidung zwischen nichtkomplexen Clifford-Quantenschaltungen und komplexen Clifford-Quantenschaltungen, um Quantenkomplexität als Kunst darzustellen. Quantenkomplexität manifestiert sich als erhöhte künstlerische Komplexität, die direkt mit entropischen Maßen quantifiziert wird. 

Shannon-Entropie

Die Entropie, insbesondere die Shannon-Entropie, ist ein Maß für die Komplexität in klassischen Systemen. Die Shannon-Entropie ist ein bekanntes Maß für fraktales Chaos und Komplexität. Sie wurde kürzlich auch als Maß für die Komplexität von Tönen in musikalischen Kompositionen vorgeschlagen (Link), wobei Beethovens Kompositionen höhere Entropiemaße aufweisen. Man beachte die Unterscheidung zwischen Entropiemaßen für klassische Systeme und Entropiemaßen für Quantensysteme. In unserer Arbeit werden klassische Kompositionen mit quantenmechanischen Wellenformen versehen, weshalb wir ein klassisches Maß für die Entropie wählen. Die Entropie wird verwendet, um die künstlerische Komplexität zwischen Kunst, die mit Clifford- und Nicht-Clifford-Quantenschaltungen erzeugt wurde, zu quantifizieren und zu unterscheiden.

Die globale Shannon-Entropie liefert eine Gesamtkomplexitätsbewertung, indem sie das gesamte System betrachtet, während die boxbasierte Shannon-Entropie eine detailliertere Sichtweise bietet, indem sie bestimmte Regionen oder Komponenten der fraktalen Kunst analysiert. Dieser duale Ansatz ermöglicht ein umfassendes Verständnis der durch Quantenprozesse erzeugten künstlerischen Komplexität. Durch die Anwendung dieser Entropiemaße können wir die komplizierten Muster, die von verschiedenen 

Quantengenerierte Kunst 

Unsere Kunst wird mit zwei Quantenschaltkreisen instanziiert, die ausgeführt werden, um die Amplitude und Phase der Quantenwellenfunktion zu extrahieren. Der Wechsel zwischen einem Clifford-Schaltkreis und einem Nicht-Clifford-Schaltkreis erfolgt einfach durch den Austausch der Pauli-Operatoren mit rotierenden Pauli-Operatoren, so dass die Komplexität tatsächlich durch die Hinzufügung von Nicht-Clifford-Operatoren und nicht durch die Einführung neuer Verschränkungsoperationen entsteht. Für die Rotation der Pauli-Operatoren wurden Fibonacci- und harmonische Reihenmuster verwendet. Die Amplituden der Wellenfunktion werden nach jeder Schaltungsschicht auf einem Quantencomputer ermittelt, während die Phasen durch klassische Simulation gewonnen werden.

© Wiktor Mazin

Wir verwenden die Ausgänge der Clifford- und Nicht-Clifford-Wellenfunktionen getrennt als Eingabe für einen einfachen SinOsc-Synthesizer, der zwei separate Songs komponiert. Die Komplexität des Nicht-Clifford-Songs ist hörbar im Vergleich zum Clifford-Song, der eine reichhaltige Struktur besitzt, die aus den rotierenden Pauli-Operationen des Schaltkreises entsteht.

Quantenkomplexität kann auch mit Hilfe der Quantenfraktalkunst visualisiert werden. Wir untersuchen diese Komplexität, indem wir Fraktalbilder direkt aus dem Schaltkreisausgang erzeugen und das Audiosignal in einen Quantenprozessor eingeben. Die linken Abbildungen sind Fraktale, die von Clifford-Quantenschaltungen erzeugt wurden, die rechten Abbildungen sind Fraktale, die von komplexen, nicht-Clifford-Quantenschaltungen erzeugt wurden. Es ist visuell erkennbar, dass die Nicht-Clifford-Quantenschaltungen und die Nicht-Clifford-Quantenklänge komplexere Fraktale erzeugen. Dies spiegelt sich auch quantitativ wider, denn die fraktalen Nicht-Clifford-Bilder haben eine größere Shannon-Entropie als die fraktalen Clifford-Bilder, siehe die drei fraktalen Bildpaare unter.1

© Wiktor Mazin

© Wiktor Mazin

© Wiktor Mazin

Bei den Bildern, die aus dem Quanten-Audio-Input generiert wurden, ist dies etwas weniger offensichtlich, aber der Trend zu höherer Entropie bleibt bestehen, siehe die Dreiergruppe der fraktalen Clifford- und Nicht-Clifford-Bilder.

© Wiktor Mazin

Das Zusammenspiel von Quantencomputern und künstlerischen Formen markiert das Aufkommen eines neuen kreativen Paradigmas. Abstrakte Konzepte wie Verschränkung und Quantenkomplexität durch die Kunst auszudrücken, ermöglicht es uns, die grundlegendsten Strukturen der Natur mit allen Sinnen zu erfassen. In dem Maße, wie sich die Quantentechnologie weiterentwickelt, werden auch unsere Möglichkeiten, mit Quantensystemen zu interagieren und sie auf immer komplexere Weise zu gestalten, zunehmen. Unsere Arbeit legt einige Grundsteine für zukünftige künstlerische Ausdrucksformen, die in der Kontrolle der Quantendynamik wurzeln. Wir formen Quantensysteme, und durch die künstlerische Form formen die Quantensysteme uns.

Autor:innen (alphabetisch): Mekena McGrew und Wiktor Mazin.
Haftungsausschluss: Dieser Artikel gibt den Standpunkt der Autoren wieder.

• 1Each image pair is generated using the same fractal mathematics, and colors are removed to not influence the entropy calculations.